Ciri Fitur dengan GLCM – Gray Level Coocurance Matrix

By | October 23, 2021
2 Comments
Print Friendly, PDF & Email
4,507 Views

Ciri Fitur dengan GLCM – Gray Level Coocurance Matrix – Manusia mengenal tekstur seperti lembut dan kasar walaupun tangan tidak menyentuh benda tersebut, tapi otak mampu membedakan  hal tersebut melalui visualisasi yang ditangkap oleh mata. Ciri fitur tersebut dapat dicirikan sebagai berikut

  1. Pengulangan pola dari variasi lokal sehingga membentuk kesatuan yang utuh
  2. Menyediakan informasi susunan spasial dari warna dan intensitas citra
  3. Dicirikan dengan distribusi spasial dari level intensitas dari nilai pixel ketetanggaan
  4. Tidak bisa didefinisikan sebagai suatu satu point / nilai tertentu karena merupakan sebuah pola / kesatuan

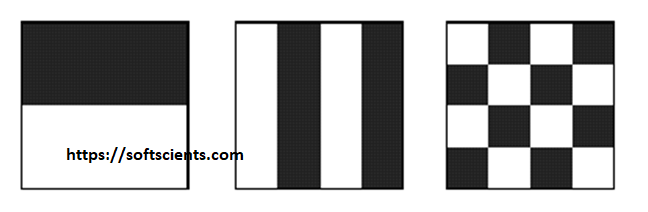
Lihatlah ilustrasi berikut tentang tekstur sebuah citra yaitu terdiri dari 50% hitam dan 50% putih

Tentunya uji statistik standar seperti mean, standar deviasi tidak akan mampu membedakan ketiga citra tersebut karena akan menghasilkan nilai yang sama. Seperti yang sudah dijelaskan bahwa tekstur merupakan suatu pengulangan pola dan distribusi spasial artinya ketiga citra tersebut mempunyai tingkat intensitas nilai pixel yang sama tapi mempunyai distribusi spasial yang berbeda.

Analisis tekstur merupakan salah satu metode untuk melakukan identifikasi atau klasifikasi suatu citra, analisis tersebut telah banyak digunakan dalam berbagai bidang yaitu uji tekstur wajah, mutu keramik, membedakan jenis daun dan dalam interpretasi suatu peta sehingga dapat diketahui jenis lahan.

 

GLCM sebagai ciri fitur

Gray-Level Co-occurrence matrix merupakan metode paling banyak digunakan untuk analisis tekstur. Metode ini diperkenalkan oleh Haralick di tahun 1973 yang merupakan bagian dari project yang didukung olah NASA yaitu tepatnya NASA Goddard Space Flight Center. Haralick menggunakan citra dari NASA ERTS untuk melakukan klasifikasi dengan tingkat akurasi diatas 80%.

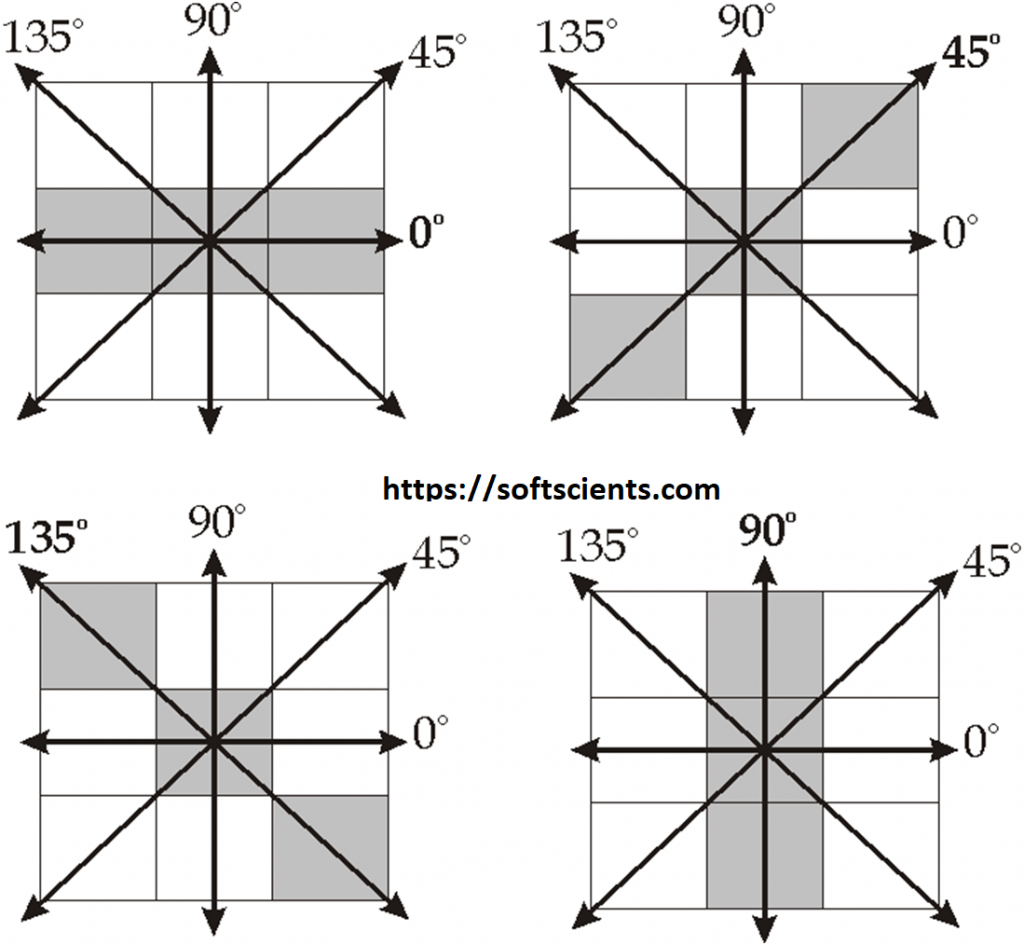
See also  Deteksi Tepi / Edge Detection

Matrix GLCM dihitung dari nilai pixel yang berpasangan dan memiliki nilai intensitas tertentu. Misalkan d adalah jarak antara dua pixel yaitu (x1,y1) dan (x2,y2) dan Ѳ tetha didefinisikan sebagai sudut antara keduanya, maka matrix GLCM merupakan distribusi spasial dari Pd Ѳ (i,j). Banyak paper menuliskan berbagai versi tentang perhitungan GLCM terutama mengenai masalah sudut yang digunakan.  Berikut adalah ilustrasi yang menggambarkan arah sudut dengan jarak 1 pixel dan ada 4 jenis sudut yang digunakan:

  1. 0o=180o;
  2. 45o=225o,
  3. 90o=270o, dan
  4. 135o=315o

tapi terkadang ada yang menyatakan terdiri dari 8 arah, hal ini terjadi karena antara sudut 0o dan 180o dianggap berbeda begitu juga dengan arah sudut yang lainnya

Cara menghitung GLCM

Misalkan kita mempunyai array dengan skala intensitas dari 0 sampai 2

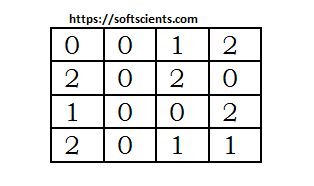
Maka tentukan P1,0(M) yaitu matrix GLCM dari jarak 1 untuk sudut 0o

[1] Buatlah matrix pasangan yaitu

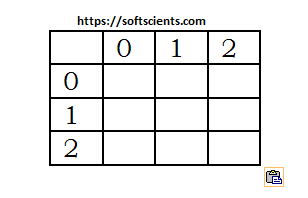
[2] Misalkan hitung matrix pasangan (0,0) untuk sudut 0 dan 180

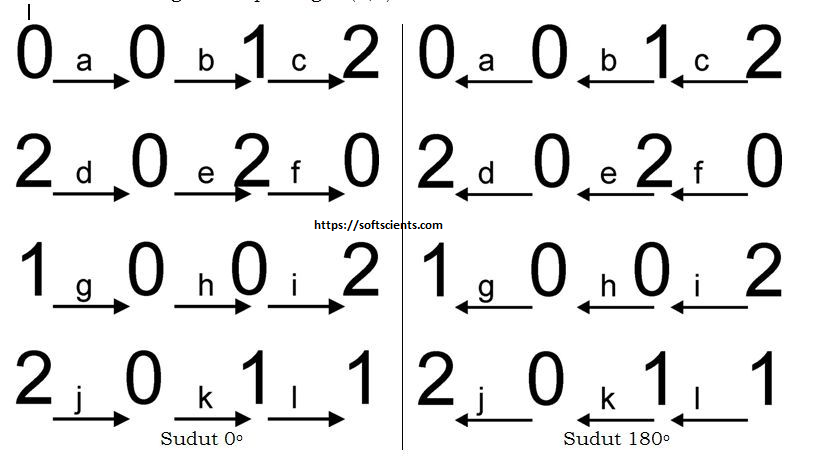
hasilnya yaitu

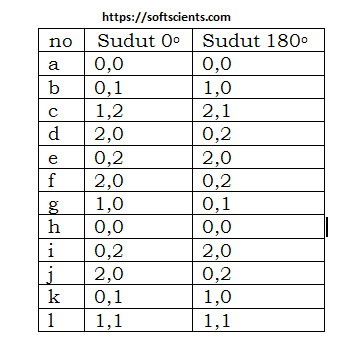
Sehingga matrix GLCM nya adalah

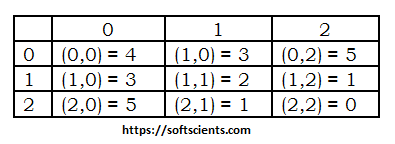
[3] Langkah selanjutnya adalah melakukan normalisasi yaitu matrixGLCMNorm. Jumlah total nilai = 24

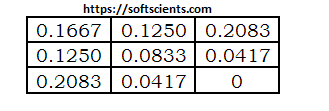
    \[matrixGLCMNorm = \frac{1}{\sum{matrixGLCM}}*matrixGLCM\]

Bila dijumlahkan akan menghasilkan nilai 1. Matrix diatas merupakan input untuk perhitungan fitur tekstur.  Berikut adalah beberapa fitur yang bisa dihitung menggunakan GLCM yaitu terdiri dari 7 fitur utama dan 7 fitur tambahan yang diturunkan dari 7 fitur utama.

  1. Angular second moment/uniformity/energy
  2. Entropy
  3. Dissimilarity
  4. Contrast/inertia
  5. Correlation
  6. Homogeneity/inverse difference moment
  7. Autocorrelation
  8. Sum of squares (variance)
  9. Sum average
  10. Sum variance
  11. Sum entropy
  12. Difference variance
  13. Difference entropy
  14. Information measures of correlation

1. Angular Second moment/uniformity/enery

    \[ f_1=\sum_i\sum_j{p(i,j)^2} \]

dengan p  adalah matrix GLCM

2. Entropy

    \[ f_2=-\sum_i\sum_j{p(i,j) \cdot log_2(p(i,j))} \]

3. Dissimilarity

    \[ f_3=\sum_i\sum_j{|i-j| \cdot p(i,j)} \]

4. Contrast / inertia

    \[ f_3=\sum_i\sum_j{(i-j)^2 \cdot p(i,j)} \]

See also  Segmentasi warna berdasarkan Color Palette

 

5. Correlation

(1)   \begin{equation*} \begin{split} f_5 = \frac{\sum_i\sum_j{(i-\mu_x) \cdot (j-\mu_y) \cdot p(i,j)}}{\sqrt{\delta_x \delta_y}}\\ \mu_x = \sum_i \sum_j{i \cdot p(i,j)}\\ \mu_y = \sum_i \sum_j{j \cdot p(i,j)} \\ \delta_x = \sum_i \sum_j{(i-\mu_x)^2 \cdot p(i,j)} \\ \delta_y = \sum_i \sum_j{(j-\mu_x)^2 \cdot p(i,j)} \\ \end{split} \end{equation*}

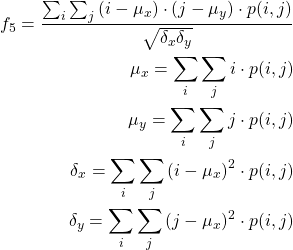
6. Homogeneity / inverse difference moment

    \[ f_6 = \sum_i \sum_j {\frac{p(i,j)}{1+(1-j)^2}} \]

7. Autocorrelation

    \[ f_7 = \sum_i \sum_j i \cdot j \cdot p(i,j) \]

 

 

  1. Angular second moment/uniformity/energy: Mengukur tentang keseragaman atau sering disebut angular second moment. Energy akan bernilai tinggi ketika nilai pixel mirip satu sama lain sebaliknya akan bernilai kecil menandakan nilai dari GLCM normalisasi adalah heterogen. Nilai maksimum dari energy adalah 1 yang artinya distribusi pixel dalam kondisi konstan atau bentuk nya yang berperiodik (tidak acak).
  2. Entropy: Mengukur kompleksitas(keacakan) citra. Entropy akan bernilai tinggi ketika citra tidak seragam.
  3. Dissimilarity: Mengukur ketidakmiripan suatu tekstur, yang akan bernilai besar bila acak dan sebaliknya akan bernilai kecil bila seragam.
  4. Contrast/inertia: Mengukur frekuensi spasial dari citra dan perbedaan moment GLCM. Perbedaan yang dimaksudkan adalah perbedaan tinggi dan rendah nya pixel.  Contrast akan bernilai 0 jika pixel ketetanggaan mempunyai nilai yang sama.
  5. Correlation: Mengukur linearitas (the  joint  probability) dari sejumlah pasangan pixel (pairs).
  6. Homogeneity/inverse difference moment: Mengukur homogenitas. Nilai ini sangat sensitif terhadap nilai disekitar diagonal utama. Bernilai tinggi ketika semua pixel mempunyai nilai yang sama / seragam.  Kebalikan dari contrast yaitu akan bernilai besar jika mempunyai nilai pixel yang sama pada saat energy bernilai tetap.
  7. Autocorrelation: Mengukur correlation diantara garis diagonal utama.

Studi Kasus GLCM

Apa yang anda pikirkan tentang hal dibawah ini!

Gambar diatas adalah gambar yang sama! gambar kiri dan gambar tengah berasal dari gambar bagian kanan.

gambar kiri dan tengah merupakan gambar yang diacak menggunakan algoritma arnold cat maps! karena berasal dari gambar yang sama! maka ketiga citra tersebut mempunyai histogram yang sama pula!

Tentunya uji stastistik biasa seperti mean dan standar deviation tidak akan mampu membedakan mereka! Mereka hanya berbeda lokasi saja! Bagaimana olah citra memandang kasus diatas! Mari kita hitung GLCM (gray level co-occurance matrix) sehingga didapatkan hitungan seperti berikut

See also  Hilangkan Duplikasi Foto

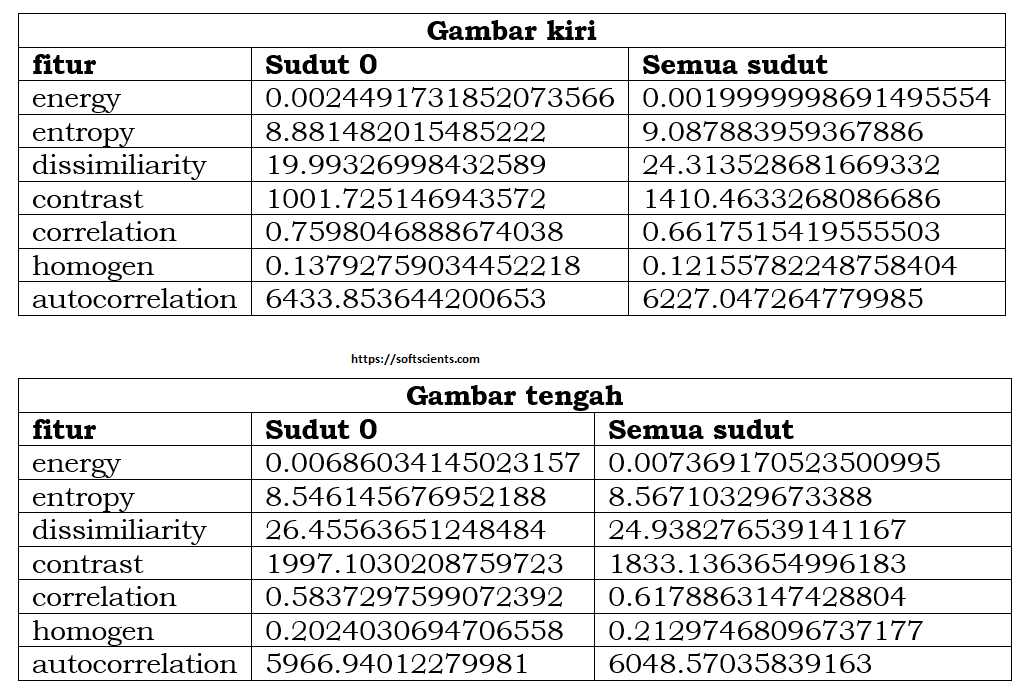
Ternyata menghasilkan perhitungan yang berbeda! Mari kita lihat tentang energy

  1. Energy: akan bernilai tinggi ketika nilai pixel mirip satu sama lain sebaliknya akan bernilai kecil menandakan nilai dari GLCM normalisasi adalah heterogen. Nilai maksimum dari energy adalah 1. Ternyata menurut GLCM diketahui bahwa yang paling seragam adalah gambar tengah  karena nilai energy mendekati angka 1
  2. Entropy: akan bernilai tinggi ketika citra tidak seragam. Jadi menurut GLCM yang tidak seragam adalah citra 1. Artinya energy akan berbanding terbalik dengan entropy!

Apakah benar tersebut!! Mari kita buktikan melalui gambar berikut ini yang diacak menggunakan algoritma logistisc maps

Lihat perhitungan berikut

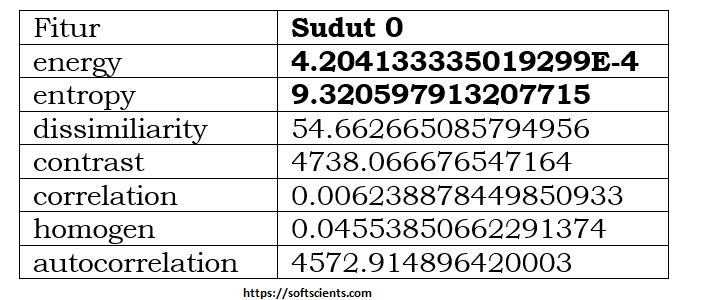
Terlihat bahwa energy bernilai sangat kecil 4.2 10- 4 angka yang menuju 0 sedangkan  entropy sangat besar yaitu 9.32 lebih besar dari gambar kiri yaitu 9.087.

Jadi apa kesimpulannya!

Ternyata GLCM bisa menilai hal diatas bahwa GLCM adalah salah satu dari analisis ciri fitur yang cukup baik

2 thoughts on “Ciri Fitur dengan GLCM – Gray Level Coocurance Matrix”

Leave a Reply