Sinopsis
Setiap pengambilan keputusan untuk memilih sesuatu, seseorang akan didasari dengan beberapa kriteria. Masing-masing kriteria mempunyai nilai tersendiri bagi seorang pengambil keputusan atau disebut pembobotan. Algoritma SAW (Simple Additive Weighting) adalah salah satu algoritma yang digunakan untuk pengambilan keputusan yang mempunyai nama lain algoritma MFEP (Multi Factor Evaluation Process).
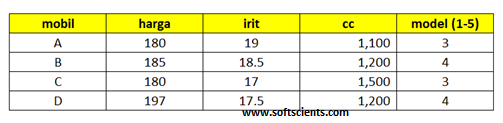
Penulis sajikan kasus sederhana berikut, dimana seorang pembeli mobil akan membandingkan beberapa jenis mobil dengan kriteria harga (dalam ratus juta rupiah), irit (jarak tempuh dalam 1 liter/km), cc, dan model (rentang 1 sampai 5)
Bobot
Masing-masing kriteria mempunyai bobot tersendiri bagi si pembeli mobil yaitu
Rule
Tentu kriteria harga yang terendah merupakan nilai yang baik bagi si pembeli, tapi berbeda dengan ke irit an, cc dan model dengan nilai yang tertinggi merupakan nilai yang terbaik. Maka sebuah rule sebagai berikut, dimana harga terendah yaitu 180 dan iri-cc-model tertinggi masing-masing 19; 1500; 4.
Normalisasi
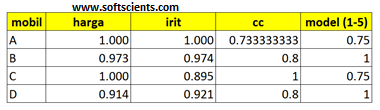
Perhitungan normalisasi sebagai berikut dikarenakan harga mempunyai aturan turun, maka rumus nya
harga = (nilai terendah)/(harga di tiap jenis mobil)
sedangkan untuk irit, cc, dan model dengan rumus berikut
(irit,cc,model) = ((irit,cc,model)di tiap jenis mobil )/(nilai maksimal (irit,cc,model))
Pembobotan
Hasil normalisasi akan dilakukan pembobotan sesuai dengan bobot yang telah ditentukan sebelumnya dengan cara dikalikan.
Pengambilan Keputusan
Hasil akhir yaitu diambil dari nilai tertinggi menghasilkan mobil merk B. Tentu kalian bisa menggunakan excel untuk melakukan perhitungan sederhana diatas, sedangkan penulis lebih suka menggunakan python dan pandas saja. Kalian masukan data berikut kedalam file excel.
import numpy as np
import pandas as pd
print '\n'*100
data = pd.read_excel('data.xlsx')
print 'Disajikan data berikut :\n',data
bobot = pd.Series(np.array([0.35,0.25,0.15,0.25]), index=[data.columns[1:5]])
print '\nBobot ditiap masing sebagai berikut:\n',bobot
min_harga = np.min(data['harga'])
max_irit = np.max(data['irit'])
max_cc = np.max(data['cc'])
max_model = np.max(data['model'])
data_normalisasi = data.copy()
data_normalisasi['harga'] = min_harga/data_normalisasi['harga']
data_normalisasi['irit'] = data_normalisasi['irit']/max_irit
data_normalisasi['cc'] = data_normalisasi['cc']/max_cc
data_normalisasi['model'] = data_normalisasi['model']/max_model
print '\nData normalisasi:\n',data_normalisasi
data_terbobot = data.copy()
data_terbobot['harga'] = data_normalisasi['harga']*bobot['harga']
data_terbobot['irit'] = data_normalisasi['irit']*bobot['irit']
data_terbobot['cc'] = data_normalisasi['cc']*bobot['cc']
data_terbobot['model'] = data_normalisasi['model']*bobot['model']
print '\nData terbobot:\n',data_terbobot
mobil = data['mobil']
hasil = pd.DataFrame(columns=['bobot'],index=[mobil])
for i in range(0,len(data)):
kriteria = ['harga','irit','cc','model']
jumlah = 0
for j in range(0,len(kriteria)):
jumlah = jumlah+data_terbobot.loc[i][kriteria[j]]
hasil.loc[mobil[i]]['bobot']=jumlah
print '\nJumlah Akhir:\n',hasil
print '\nHasil terbesar adalah :\n'
print hasil[hasil['bobot']==np.max(hasil['bobot'])]
hasil
Disajikan data berikut :
mobil harga irit cc model
0 A 180 19.0 1100 3
1 B 185 18.5 1200 4
2 C 180 17.0 1500 3
3 D 197 17.5 1200 4
Bobot ditiap kriteria sebagai berikut:
harga 0.35
irit 0.25
cc 0.15
model 0.25
dtype: float64
Data normalisasi:
mobil harga irit cc model
0 A 1.000000 1.000000 0.733333 0.75
1 B 0.972973 0.973684 0.800000 1.00
2 C 1.000000 0.894737 1.000000 0.75
3 D 0.913706 0.921053 0.800000 1.00
Data terbobot:
mobil harga irit cc model
0 A 0.350000 0.250000 0.11 0.1875
1 B 0.340541 0.243421 0.12 0.2500
2 C 0.350000 0.223684 0.15 0.1875
3 D 0.319797 0.230263 0.12 0.2500
Jumlah Akhir:
bobot
mobil
A 0.8975
B 0.953962
C 0.911184
D 0.92006
Hasil terbesar adalah :
bobot
mobil
B 0.953962