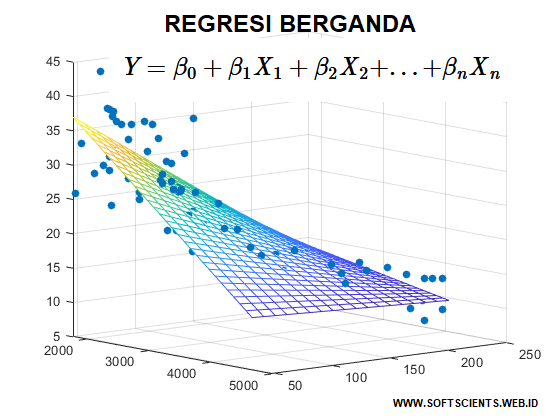
Setelah kalian belajar mengenai regresi linear sederhana disini, tentu akan timbul problem yang lainnnya yaitu tidak semua permasalahan 2 variabel saja pada kondisi real dilapangan, misalkan saja beberapa variabel akan mempengaruhi variabel output, nah untuk topik ini dipecahkan menggunakan Regresi Linear Berganda. Secara umum Regresi Linear Berganda / Multi Regression bekerja dengan persamaan umum sebagai berikut
![]()
atau dalam persamaan umum yang lainya menjadi
![]()
Karena cukup rumit, contoh kasusnya yaitu 2 variabel saja yaitu ![]() dan
dan ![]() , maka untuk perhitungan regresi berganda yaitu
, maka untuk perhitungan regresi berganda yaitu
Metode 1
Contents
jika ![]() dan
dan ![]() adalah data-data vektor/array, maka
adalah data-data vektor/array, maka
![]()
![]()
dengan ![]() dan
dan ![]() adalah rerata
adalah rerata
(1) 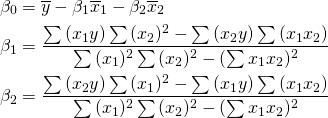
Metode 2
atau dalam persamaan yang lainnya untuk mencari ![]() ,
, ![]() , dan
, dan ![]() yaitu
yaitu
(2) 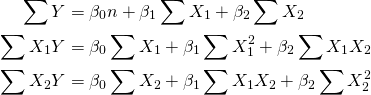
kalian bisa ubah kedalam persamaan array
![]()
yaitu
![Rendered by QuickLaTeX.com \[A=\begin{pmatrix} n & \sum{X_1} & \sum{X_2} \\ \sum{X_1} & \sum{X_1^2} & \sum{X_1X_2} \\ \sum{X_2} & \sum{X_1X_2} & \sum{X_2^2} \\ \end{pmatrix}, \beta = \begin{pmatrix} \beta_0 \\ \beta_1 \\ \beta_2 \\ \end{pmatrix}, H = \begin{pmatrix} \sum{Y} \\ \sum{X_1Y}\\ \sum{X_2Y} \end{pmatrix}\]](https://softscients.com/wp-content/ql-cache/quicklatex.com-a3dbb3034c1d7fd914510f1bc19baee4_l3.png)
gampang sekali untuk mencari ![]() dengan cara, jika
dengan cara, jika ![]() , maka
, maka
![]()
Dataset
Mari coba dengan dataset berikut ini yang merupakan contoh harga saham tahunan untuk mengetahui pengaruhn PER (price earning ratio) dan ROI (return on investment).
>> data
data =
11×4 table
tahun harga per roi
_____ _____ ___ ___
2003 8300 5 6
2004 7500 3 5
2005 8950 4 4
2006 8250 5 6
2007 9000 4 3
2008 8750 3 5
2009 9500 5 6
2010 8500 6 4
2011 8350 4 6
2012 9500 6 5
2013 9750 7 6
>>
Sebagai variabel Y yaitu harga, sedangkan x1 yaitu per; serta x2 yaitu roi, maka dari dataset diatas didapatkan hasil berikut
A =
11 52 56
52 262 268
56 268 296
H =
96350
460450
490450
Dan ![]() nya sebagai berikut
nya sebagai berikut
beta_0 = 7.7351e+03 beta_1 = 328.6184 beta_2 = -104.0022
Sangat mudah sekali bukan? Penulis kasih kodenya yang lebih lengkap sesuai dengan persamaan/cara no 2 yang digunakan dibawah ini
Kode Lengkap Matlab
Kalian bisa coba dengan kode berikut untuk Regresi Linear Berganda
clc;clear all;close all; format compact; format short;
data = readtable('data.csv')
y = data.harga; %target
x1 = data.per;
x2 = data.roi;
%ubah menjadi persamaan array/matrix
n = length(y);
A = [n, sum(x1), sum(x2);
sum(x1), sum(x1.^2), sum(x1.*x2);
sum(x2), sum(x1.*x2), sum(x2.^2)]
H = [sum(y); sum(x1.*y); sum(x2.*y)]
%hitung nilai beta
beta = inv(A)*H;
%hasil beta
beta_0 = beta(1)
beta_1 = beta(2)
beta_2 = beta(3)
Maka dari hasil diatas, persamaan nya menjadi
![]()
menjadi
![]()
Prediksi
Tentu kalian akan membandingkan kinerja regresi berganda untuk melakukan prediksi dan targetnya, cara mudahnya menggunakan plot saja
y2 = beta_0+beta_1*x1+beta_2*x2;
figure
hold on
plot(y);
plot(y2);
xlabel('data ke n'),ylabel('harga')
grid on
legend('Target','Prediksi')
title('Regresi Berganda')
Menghitung Regresi Berganda dengan Jumlah Variabel lebih dari 2
Sedangkan untuk jumlah variabel lebih 2, maka rumusnya sebagai berikut, misalkan untuk 4 variabel
(3) 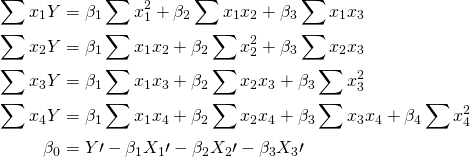
dengan ![]() dan
dan ![]() adalah rerata, sebelum kalian memasukan kedalam persamaan diatas, maka perlu kalian hitung dulu
adalah rerata, sebelum kalian memasukan kedalam persamaan diatas, maka perlu kalian hitung dulu
(4) 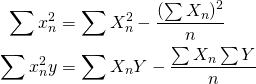
Makin banyak sekali dan membuat kalian bisa pusing, nah mendingan kita gunakan saja function ![]() bawaan Matlab untuk Multi Regression nya
bawaan Matlab untuk Multi Regression nya
Multi Regression dengan Matlab
Untuk di Matlab kalian bisa menggunakan ![]() yang dapat digunakan untuk Multi Regression. Cobalah kode dibawah ini yang sangat simple sekali digunakan.
yang dapat digunakan untuk Multi Regression. Cobalah kode dibawah ini yang sangat simple sekali digunakan.
clc;clear all;close all; format compact; format short;
data = readtable('data.csv')
y = data.harga; %target
X = [data.per,data.roi]; %prediktor
model = fitlm(X,y)
hasilnya
data =
11×4 table
tahun harga per roi
_____ _____ ___ ___
2003 8300 5 6
2004 7500 3 5
2005 8950 4 4
2006 8250 5 6
2007 9000 4 3
2008 8750 3 5
2009 9500 5 6
2010 8500 6 4
2011 8350 4 6
2012 9500 6 5
2013 9750 7 6
model =
Linear regression model:
y ~ 1 + x1 + x2
Estimated Coefficients:
Estimate SE tStat pValue
________ ______ ________ __________
(Intercept) 7735.1 1052.6 7.3488 8.0029e-05
x1 328.62 152.35 2.157 0.063081
x2 -104 185.55 -0.56051 0.59048
Number of observations: 11, Error degrees of freedom: 8
Root Mean Squared Error: 594
R-squared: 0.368, Adjusted R-Squared 0.21
F-statistic vs. constant model: 2.33, p-value = 0.16
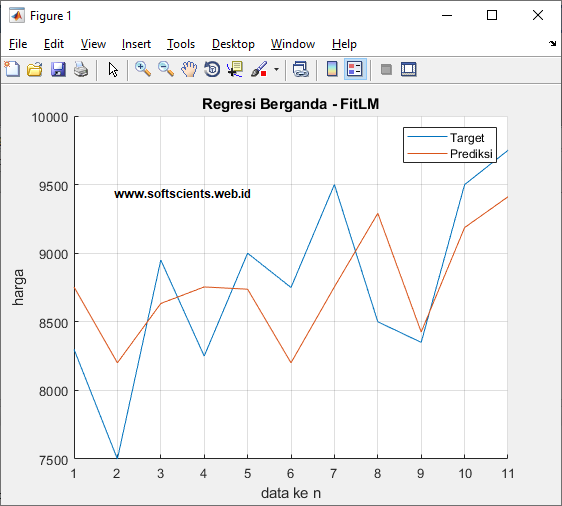
Prediksi
Tentu kalian akan membandingkan kinerja regresi berganda untuk melakukan prediksi dan targetnya, cara mudahnya menggunakan plot saja dan function ![]()
y2 = predict(model,X);
figure
hold on
plot(y);
plot(y2);
xlabel('data ke n'),ylabel('harga')
grid on
legend('Target','Prediksi')
title('Regresi Berganda - FitLM')
Pada pembahasan ini kalian sudah belajar mengenai kasus-kasus yang bersifat linear menggunakan Regresi Berganda.