Belajar Matlab – Fungsi Polynomial

By | January 14, 2021
0 Comment
Print Friendly, PDF & Email
3,261 Views

Function Tools adalah evaluasi sebuah function, yang bisa digunakan untuk mencari F(x)=0, mencari nilai maksimal, dan minimal, serta interpolasi data. Kita akan bahas satu-persatu

Evaluasi Fungsi Polynomial

Sebuah persamaan fungsi polynomial berbentuk sebagai berikut yang diurutkan berdasarkan orde n tinggi sampai ke rendah

    \[p(x)=a_nx^n+a_{n-1}x^{n-1}+a_1+a_0\]

Misalkan kita punya persamaan sebagai berikut

    \[g(x)=2x^3+5x-1\]

atau ditulis sebagai

    \[g(x)=2x^3+0x^2+5x-1\]

Dari persamaan diatas berapa nilai g(10)? Untuk mencari hasil diatas cukup menggunakan perintah polyval(f,x) function tersebut juga bisa menerima sebuah array koq

clc;clear all;close all;
g = [2,0,5,-1];
x = 10;
x2 = 1:10;
 
a = polyval(g,x)
b = polyval(g,x2)

hasil

a =

        2049


b =

  Columns 1 through 5

           6          25          68         147         274

  Columns 6 through 10

         461         720        1063        1502        2049

Perkalian Polynomial

Tidak sampai disitu saja, kalian juga bisa melakukan perkalian antar polynomial lho, misalkan perkalian antara g(x) dan h(x) dibawah ini

    \[h(x)=6x^2-7\]

Cukup menggunakan perintah conv(g,h) yang akan diporoleh sebuah persamaan baru lagi, kita sebut saja p(x)

clc;clear all;close all;
g = [2,0,5,-1];
h = [6,0,-7];
p = conv(g,h)

hasil

p =

    12     0    16    -6   -35     7

    \[p(x)=12x^5+16x^3-6x^2-35x+7\]

Contoh lain berikut yang akan membuat persamaan kuadrat orde 2

    \[a(x)=x-2\]

    \[b(x)=x+4\]

Perkalian diatas menghasilkan

    \[c(x)=x^2+2x-8\]

clc;clear all;close all;
a = [1,-2];
b = [1,4];
c = conv(a,b)

hasil

c =

     1     2    -8

Mencari akar Persamaan Polynomial

Untuk mencari akar persamaan kuadrat sangatlah mudah, yaitu untuk mengitung f(x)=0, agar mudah gunakan persamaan diatas

    \[c(x)=x^2+2x-8\]

Berapa nilai akar persamaan kuadrat diatas? Cukup gunakan perintah roots()

clc;clear all;close all;
c = [1,2,-8];
d = roots(c)

hasil

d =

    -4
     2

Turunan Pertama dari Persamaan Polynomial

Turunan pertama atau fungsi derifatif, sangat mudah dilakukan di Matlab yaitu cukup dengan perintah polyder(), misalkan turunan pertama dari

    \[c(x)=x^2+2x-8\]

Adalah

    \[c'(x) = 2x+2\]

Bila kita turunkan lagi menjadi

    \[c''(x) = 2\]

Kita coba saja yuk

clc;clear all;close all;
c = [1,2,-8];
c1 = polyder(c)
c2 = polyder(c1)

hasil

c1 =

     2     2


c2 =

     2

Bagaimana menurut kalian cara melakukan operasi pada fungsi polynomial di matlab? Sangat mudah bukan

Mencari Nol dari Fungsi

Pada pembahasan sebelumnya untuk mencari nol dari fungsi polynomial menggunakan perintah root(), sedangkan ada perintah lain berupa fzero() yang membutuhkan sebuah tebakan awal/initial value karena perintah ini menggunakan algoritma iteratif. Agar mudah, kita akan gunakan persamaan diatas yang dibuat sebuah anonymous function dan sedikit perubahan agar bisa menerima input berupa vector/array

    \[c(x)=x^2+2x-8\]

Oiya kenapa kita menggunakan anonymous bukan dibuat sebuah script? Karena fungsi tersebut bersifat lokal serta hanya perlu 1 baris saja sehingga menghemat tempat dan tidak kebanyakan script

y = @(x) x.^2+2*x-8; %ini adalah fungsi anonymous

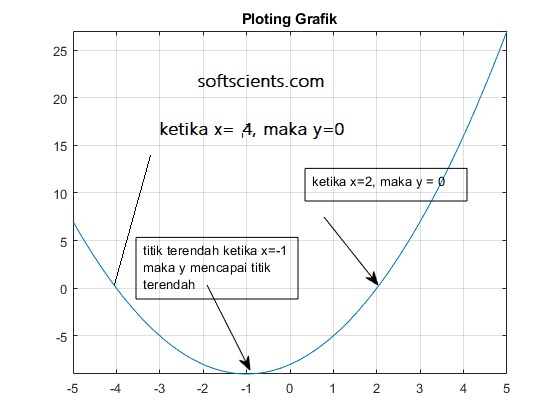
Untuk mentukan sebuah tebakan awal, sebaiknya kita buat sebuah plot dengan perintah fplot(), mari kita coba dengan sebuah array  x=[-5,5]

clc;clear all;close all;
y = @(x) x.^2+2*x-8; %ini adalah fungsi anonymous
x = [-5,5];
fplot(y,x);
grid on
title('Ploting Grafik')

Malahan dengan plot diatas, kita mendapat sebuah informasi titik global minimalnya juga serta ada 2 nilai x yang akan menghasilkan nilai y =0, kita coba saja perintah berikut dengan tebakan awal -5 dan 0

nol_1 = fzero(y,-5)
nol_2 = fzero(y,0)

Maka hasilnya sebagai berikut

nol_1 =

    -4

nol_2 =

     2

Mencari global minimum dari fungsi

Misalkan kita ingin mencari minimum x_{min} dari fungsi f(x).

    \[f(x_{min)}=minf(x)\]

Metode iteratif ini membutuhkan tebakan awal x_0. Dari nilai awal ini akan diperoleh nilai berikutnya, x_1, yang diharapkan semakin mendekati x_{min}. Seberapa dekat x_1 ke x_{min} tergantung pada metode numerik yang digunakan. Proses iterasi ini berlanjut hingga nilai x_{i} yang mendekati dengan akurasi tertentu diperoleh, di mana |x_{min} - x_{i}| cukup kecil.

Oiya Dalam MATLAB tidak ada command untuk menentukan maksimum suatu fungsi f(x), namun dalam hal ini bisa digunakan fungsi g(x) = − f(x) untuk dicari minimumnya. Perintah yang digunakan untuk mencari sebuah nilai minimal dengan nilai rentang tertentu yaitu fminbnd(fun,x1,x2). Kita coba saja buktikan apakah hasilnya sesuai dengan plot diatas bila menggunakan persamaan

    \[c(x)=x^2+2x-8\]

Nilai range x_1=-5 dan x_2=5

minimal = fminbnd(y,-5,5)

hasilnya

minimal =

   -1.0000

Artinya bahwa ketika x=-1 maka nilai y akan mempunyai nilai global minimal

Mencari global minimum dari banyak variabel fungsi

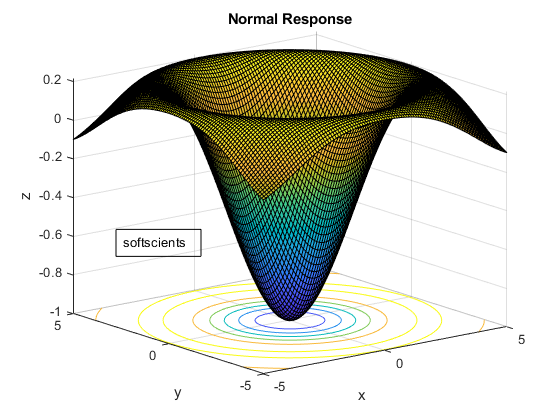
Perhatikan gambar surface berikut

clc;clear all;close all;
y = -5:0.1:5;
x = -5:0.1:5;
[X, Y] = meshgrid(x, y);
Z = - (sin(sqrt(X.^2+Y.^2)) ./ sqrt(X.^2+Y.^2));
figure
surfc(X, Y, Z)
view(-38, 18)
title('Normal Response')
xlabel('x')
ylabel('y')
zlabel('z')

Merupakan sebuah hasil dari persamaan sebagai berikut

    \[z(x,y) = -\frac{sin(\sqrt{x^2+y^2})}{\sqrt{x^2+y^2}}\]

Mempunyai nilai minimum z(x,y) = -1, pertanyaannya yaitu berapa nilai x dan y nya? Nah untuk membuat function harus kita ubah menjadi sebuah array x dan y diubah menjadi x(1) dan x(2), sedangkan perintah yang digunakan untuk mencari global minimal dengna perintah fminsearch(). Sesuai dengan informasi diatas, tebakan awal yaitu 0 sampai dengan 1

%anonymous function
g = @(x) -(sin(sqrt(x(1).^2+x(2).^2)) ./ sqrt(x(1).^2+x(2).^2));
hasil = fminsearch(g,[0,1])
g(hasil)

hasil

hasil =

   1.0e-04 *

    0.2469    0.2056


ans =

   -1.0000

 

 

Leave a Reply