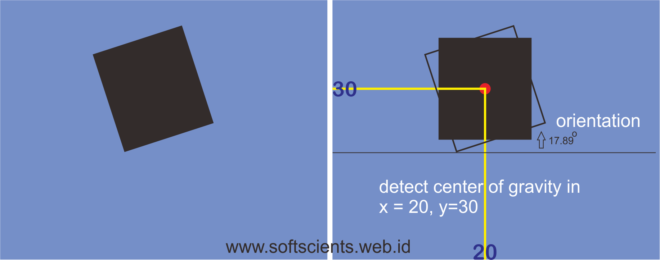
Center Of Gravity dan Orientation Image

1,928 Views

Membahas operasi morfologi/bentuk, kalian harus tahu juga cara kerja menentukan sebuah center of gravity dari sebuah objek dan Orientation nya, setelah kalian pelajari Buku Pengolahan Citra Digital dengan Matlab – Segmentasi, kalian tentu ingin tahu cara kerja/kode tersebut secara lebih simple. Pembahasan ini dalam 1 topik geometri moment invariant

operasi blob/labelling untuk menentukan jumlah objek
menentukan lokasi centroid untuk masing-masing objek
menentukan orientation nya

Perhitungan Center of Gravity

Perhitungan center of gravity banyak digunakan pada computer vision salah satunya dalam membuat aplikasi scanner Membuat Scanner Document Corner Detection OpenCV Java

Untuk mempermudah kalian pelajari, disajikan 1 buah gambar kotak putih yang punya orientasi miring 18 derajat.

Moment

Moment suatu objek dapat menggambarkan luas area, posisi, orientasi dengan persamaan sebagai berikut

$m_{ij}=\sum_{x}\sum_{y}x^i*y^j*a_{xy}$

Dengan $i$ dan $j$ adalah posisi pixel dengan intensitas $a_{xy}$ . Moment tingkat 0 dan 1 didefinisikan sebagai berikut

$m_{00}=\sum_{x}\sum_{y}a_{xy}$

$m_{10}=\sum_{x}\sum_{y}x*a_{xy}$

$m_{01}=\sum_{x}\sum_{y}y*a_{xy}$

titik pusat \ center of gravity $x\prime$ dan $y\prime$ sebagai berikut

$x\prime=\frac{m_{10}}{m_{00}}$

$y\prime=\frac{m_{01}}{m_{00}}$

clc;clear all;close all;
I = imread('orientasi.png');
objek = im2bw(I);
%untuk menentukan lokasi centroid dari matrix biner
area = sum(sum(objek));
if area==0
    X = 0;
    Y = 0;
else
    [rows,cols] = size(objek);
    x = ones(rows,1)*[1:cols] ;  % Matrix with each pixel set to its x coordinate
    y = [1:rows]'*ones(1,cols) ;  %   "     "     "    "    "  "   "  y    "
 
    X= sum(sum(double(objek).*x))/area;
    Y= sum(sum(double(objek).*y))/area;
end
figure
imshow(objek)
text(X,Y,'*','Color','red','FontSize',30);
title('Center of Gravity')

Orientasi

Untuk perhitungan orientasi bisa kalian pelajari melalui kode berikut

clc;clear all;close all;
I = imread('orientasi.png');
objek = im2bw(I);
[rows,cols]=size(objek);
%calculating moment calculation%
[rows,cols] = size(objek);
x = ones(rows,1)*[1:cols];    
y = [1:rows]'*ones(1,cols);   
 
area = sum(sum(objek));
meanx = sum(sum(double(objek).*x))/area;
meany = sum(sum(double(objek).*y))/area;
 
%calculating the ellipse orientation
m20 = sum(sum(double(objek).*x.^2));
m02 = sum(sum(double(objek).*y.^2));
m11 = sum(sum(double(objek).*x.*y));
u20 = (m20/area) - (meanx^2);
u02 = (m02/area) - (meany^2);
u11 = (m11/area) - (meanx*meany);
 
tetha = 0.5*atan(2*u11/(u20-u02));
tetha= tetha*57.2957795
 
 
rotasi=imrotate(objek,tetha);
figure
subplot(1,2,1),imshow(objek),title('Asli');
subplot(1,2,2),imshow(rotasi),title(['Rotasi sebesar ' num2str(tetha)]);

Kalian bisa melihat penentuan orientasi sangat bisa diandalkan menggunakan rumus diatas, hanya berbeda sebesar $18-17.9454= 0.0546$ saja! Penerapan algoritma diatas banyak digunakan untuk scanner digital untuk deteksi arah rotasi serta melakukan operasi rotasi secara tepat!