Tepi (edge) adalah perubahan nilai intensitas derajat keabuan yang cepat/tiba-tiba (besar) dalam jarak yang singkat. Sedangkan deteksi tepi (Edge Detection) pada suatu citra adalah suatu proses yang menghasilkan tepi-tepi dari obyek-obyek citra, tujuannya adalah untuk
- menandai bagian yang menjadi detail citra; dan
- memperbaiki detail dari citra yang kabur, yang terjadi karena error atau adanya efek dari proses akuisisi citra.
Suatu titik (x,y) dikatakan sebagaitepi (edge) dari suatu citra bila titik tersebut mempunyai perbedaan yang tinggi dengan tetangganya.
Proses pendeteksian tepi citra digital dapat dilakukan dengan teknik konvolusi menggunakan berbagai macam metode/operator. Operator deteksi tepi merupakan alat yang digunakan untuk memodifikasi nilai derajat keabuan sebuah titik berdasarkan derajat keabuan titik-titik yang ada disekitarnya (konvolusi/operasi ketetanggaan). Titik-titik yang dilibatkan dalam operasi ketetanggaan tersebut diberikan bobot yang nilainya tergantung pada operasi yang akan dilakukan, sedangkan banyaknya titik yang dilibatkan biasanya 2×2, 3×3, 5×5, 7×7 dan seterusnya.
Operator yang dapat digunakan untuk deteksi tepi adalah operator
- berbasis Gradient (turunan pertama) seperti Robert, Sobel, Prewitt dan
- operator berbasis turunan kedua seperti Laplacian dan Laplacian of Gaussian.
Metode yang banyak digunakan untuk proses deteksi tepi adalah metode Robert, Prewitt dan Sobel (Gonzalez dan Woods, 2002). Namun tidak menutup kemungkinan guna memperoleh hasil deteksi tepi citra yang lebih baik (jelas), operator-operator yang ada tersebut dikombinasikan dan dikembangkan dengan teknik-teknik tertentu.
Operator Sobel
Operator Sobel menggunakan kernel ukuran 3×3 piksel. Operator Sobel melakukan deteksi tepi dengan memperhatikan tepi vertical dan horizontal.
![Rendered by QuickLaTeX.com \[ h_x= \begin{pmatrix} -1 & 0 & 1\\ -2 & 0 & 2\\ -1 & 0 & 1\\ \end{pmatrix} , h_y \begin{pmatrix} -1 & -2 & -1\\ 0 & 0 & 0\\ 1 & 2 & 1\\ \end{pmatrix} \]](https://softscients.com/wp-content/ql-cache/quicklatex.com-0c1645c4a1f00cdbe9253bc1cfe7da9c_l3.png)
Adapun untuk menghitun gradient dan orientasinya yaitu
![]()
![]()
Kita coba saja menggunakan matlab/octave
clc;clear all;close all;
%% lebih lanjut
%% http://www.generation5.org/content/2002/im01.asp
%% http://en.wikipedia.org/wiki/Sobel_operator
I = imread('D:/citra fft.jpg');
if ndims(I)==3
I = rgb2gray(I);
end
% hx = [3 10 3;0 0 0;-3 -10 -3];
hx = [ -1 0 +1;
-2 0 +2;
-1 0 +1];
hy = transpose(hx);
conv_x = (conv2(double(I),hx));
conv_y = (conv2(double(I),hy));
figure,
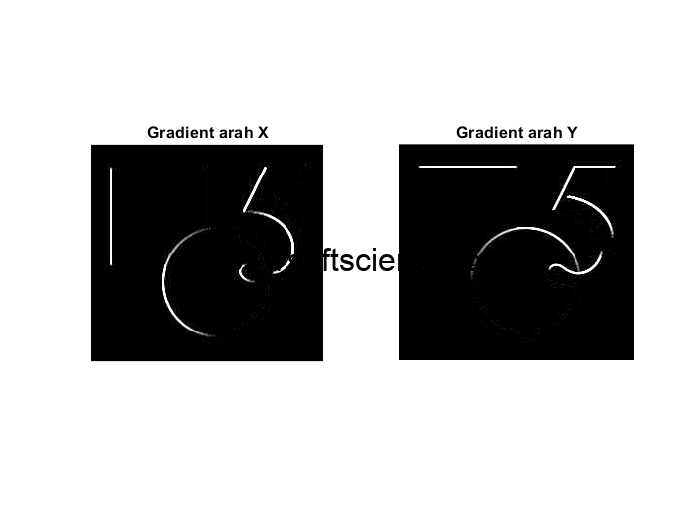
subplot(1,2,1),imshow(uint8(conv_x)),title('Gradient arah X -- www.softscients.web.id');
subplot(1,2,2),imshow(uint8(conv_y)),title('Gradient arah Y -- www.softscients.web.id');
%% gradient vektor
% hitung_gradient_vektor = abs(conv_x)+abs(conv_y);
%% gradient magnitude
hitung_gradient_magnitude = sqrt(conv_x.^2 + conv_y.^2);
%% hitung arah gradient
hitung_arah_gradient = atan2(conv_x,conv_y);
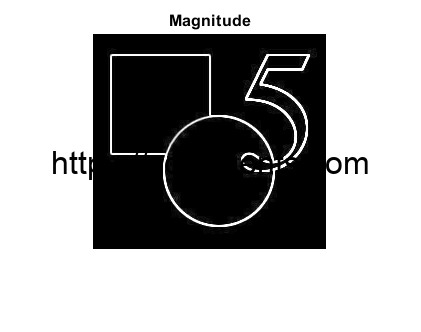
figure,imshow((uint8(hitung_gradient_magnitude))),title('Gradient Magnitude -- www.softscients.web.id');