Pengertian dan Penjelasan Deteksi Autokorelasi

3,458 Views

Deteksi Autokorelasi – Kalau membahas mengenai regresi linear, maka setidaknya ada 5 jenis asumsi yang harus kalian lakukan Normalitas, Linearitas, Multikolinearitas, Autokolinearitas, Heteroskedastisitas. Tapi pada sesi ini saya hanya akan membahas mengenai autokolerasi saja yang mana pada asumsi regresi klasik dikatakan bahwa kesalahan atau gangguan yang masuk kedalam fungsi regresi populasi adalah random atau tak berkorelasi.

Jika asumsi ini dilanggar, masalah yang muncul adalah terjadi autokorelasi. Autokorelasi dapat didefinisikan sebagai adanya korelasi antar galat atau dapat terjadi ketika kovarians dan korelasi antar galat tidak sama dengan nol. Uji autokorelasi bertujuan untuk mengetahui apakah dalam suatu model regresi linier ada korelasi antar kesalahan pengganggu (residual = $u_i$ ) pada periode t dengan kesalahan pengganggu pada periode t-1 (periode sebelumnya) biasa disebut dengan lag. Berikut beberapa pemahaman mengenai istilah diatas, maka kita akan kembali kepada regresi linear, misalkan data berikut (data produksi.xlsx)

Data Produksi

Contents

0.1 Data Produksi

1 Autokorelasi pada Regresi Linear
2 Deteksi Autokorelasi dengan Grafik ACF
- 2.1 Grafik ACF
3 Statistik Uji Durbin-Watson
- 3.1 Download Tabel Durbin Watson

tahun	Y	X
1.990	529,00	303,00
1.991	538,00	309,00
1.992	549,00	309,00
1.993	582,00	334,00
1.994	60,00	351,00
1.995	634,00	373,00
1.996	682,00	41,00
1.997	78,00	449,00
1.998	847,00	465,00
1.999	906,00	503,00
2.000	982,00	535,00
2.001	1.017,00	528,00
2.002	1.027,00	559,00
2.003	1.083,00	63,00
2.004	1.247,00	73,00
2.005	1.579,00	848,00
2.006	1.582,00	866,00
2.007	1.702,00	989,00
2.008	180,00	1.108,00
2.009	198,00	1.247,00

Generated by wpDataTables

dengan keterangan sebagai berikut

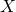$X$ adalah variabel independen dan
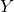$Y$ adalah variabel dependen,

Kita bisa hitung regresi linear – Pengertian dan Penjelasan Regresi Linear dengan cara berikut

library(dplyr)
library(tidyverse)
library(readxl)

#loading dataset
produksi=read_excel('data produksi.xlsx')

model = lm (formula = Y ~ X, data = produksi)
summary(model)

hasil

Call:
lm(formula = Y ~ X, data = produksi)

Residuals:
    Min      1Q  Median      3Q     Max 
-12.013  -3.386  -1.468   2.779  12.965 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  6.62427    3.32688   1.991   0.0619 .  
X            1.63103    0.05093  32.022   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 6.272 on 18 degrees of freedom
Multiple R-squared:  0.9827,	Adjusted R-squared:  0.9818 
F-statistic:  1025 on 1 and 18 DF,  p-value: < 2.2e-16

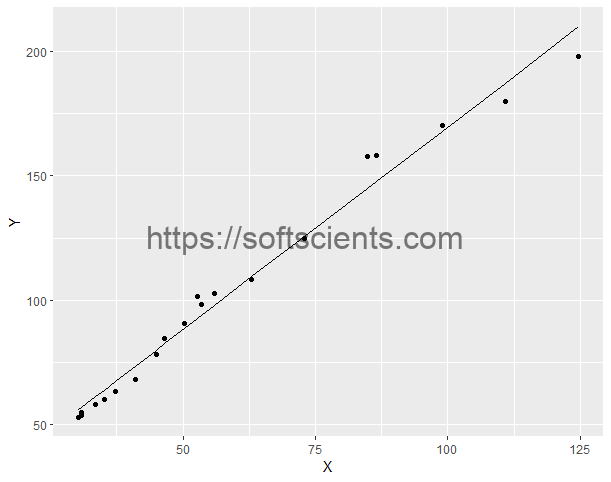
Sesuai dengan hasil diatas, didapatkan persamaan Regresi Linear yaitu

$Y=6.62427+1.63103X$

serta nilai R sebesar 0.987 (mendekati 1 berarti semakin linear). Biar lebih jelas

library(ggplot2)
ggplot() +
    geom_point(data = produksi, aes(x=X,y=Y))+
    geom_line(data=produksi,aes(x=X,y=model$fitted.values))

Autokorelasi pada Regresi Linear

Asumsi yang digunakan pada regresi linear yaitu tidak adanya korelasi. Uji autokorelasi bertujuan untuk mengetahui apakah dalam suatu model regresi linier ada korelasi antar kesalahan pengganggu (residual = $u_i$ ) pada periode t dengan kesalahan pengganggu pada periode t-1 (periode sebelumnya).

Kita bahas sebelumnya

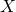$X$ adalah variabel independ
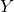$Y$ adalah variabel dependen
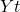$Yt$ adalah hasil prediksi regresi linear

dengan persaman regresi linear $Y=6.62427+1.63103X$ maka melalui persamaan tersebut dapat dicari nilai prediksi $Yt=6.62427+1.63103X$ . Atau bisa cari dengan kode berikut

Yt = predict(model,produksi)

Residual atau $ut$ dapat dicari dengan mencari selisih yaitu $ut=Y-Yt$

ut = Y-Yt

Sedangkan jeda/lag autokorelasi dapat dicari dengan membuat selisih nilai $ut$ sebelumnya. Yuk kita buat permudah saja seperti berikut dulu. Misalkan dibuat dulu data frame produksi2

produksi2 = data.frame(X,Y,Yt,ut)

hasil tabel diatas yaitu

       X     Y        Yt          ut
1   30.3  52.9  56.04439  -3.1443873
2   30.9  53.8  57.02300  -3.2230036
3   30.9  54.9  57.02300  -2.1230036
4   33.4  58.2  61.10057  -2.9005712
5   35.1  60.0  63.87332  -3.8733172
6   37.3  63.4  67.46158  -4.0615767
7   41.0  68.2  73.49638  -5.2963768
8   44.9  78.0  79.85738  -1.8573823
9   46.5  84.7  82.46703   2.2329744
10  50.3  90.6  88.66493   1.9350716
11  53.5  98.2  93.88421   4.3157850
12  52.8 101.7  92.74250   8.9575040
13  55.9 102.7  97.79868   4.9013201
14  63.0 108.3 109.37897  -1.0789720
15  73.0 124.7 125.68924  -0.9892425
16  84.8 157.9 144.93536  12.9646382
17  86.6 158.2 147.87121  10.3287895
18  98.9 170.2 167.93284   2.2671568
19 110.8 180.0 187.34207  -7.3420652
20 124.7 198.0 210.01334 -12.0133412

mencari nilai $lag(ut,1)$

produksi2 = produksi2 %>% mutate(ut1=lag(ut,1))

kita tampilkan

       X     Y        Yt          ut        ut1
1   30.3  52.9  56.04439  -3.1443873         NA
2   30.9  53.8  57.02300  -3.2230036 -3.1443873
3   30.9  54.9  57.02300  -2.1230036 -3.2230036
4   33.4  58.2  61.10057  -2.9005712 -2.1230036
5   35.1  60.0  63.87332  -3.8733172 -2.9005712
6   37.3  63.4  67.46158  -4.0615767 -3.8733172
7   41.0  68.2  73.49638  -5.2963768 -4.0615767
8   44.9  78.0  79.85738  -1.8573823 -5.2963768
9   46.5  84.7  82.46703   2.2329744 -1.8573823
10  50.3  90.6  88.66493   1.9350716  2.2329744
11  53.5  98.2  93.88421   4.3157850  1.9350716
12  52.8 101.7  92.74250   8.9575040  4.3157850
13  55.9 102.7  97.79868   4.9013201  8.9575040
14  63.0 108.3 109.37897  -1.0789720  4.9013201
15  73.0 124.7 125.68924  -0.9892425 -1.0789720
16  84.8 157.9 144.93536  12.9646382 -0.9892425
17  86.6 158.2 147.87121  10.3287895 12.9646382
18  98.9 170.2 167.93284   2.2671568 10.3287895
19 110.8 180.0 187.34207  -7.3420652  2.2671568
20 124.7 198.0 210.01334 -12.0133412 -7.3420652

kita sederhanakan lagi yaitu mencari regresi linear dari residual diatas

produksi2 = produksi2 %>% select(ut,ut1) %>% na.omit()
produksi2

Deteksi Autokorelasi dengan Grafik ACF

Secara umum deteksi autokorelasi ada 2 cara yaitu metode grafik (ACF) dan analitis (durbin-watson). Untuk metode grafik bisa menggunakan plot residualnya. Berikut jenis-jenis autokorelasi yaitu

1. Autokorelasi Positif seperti grafik berikut

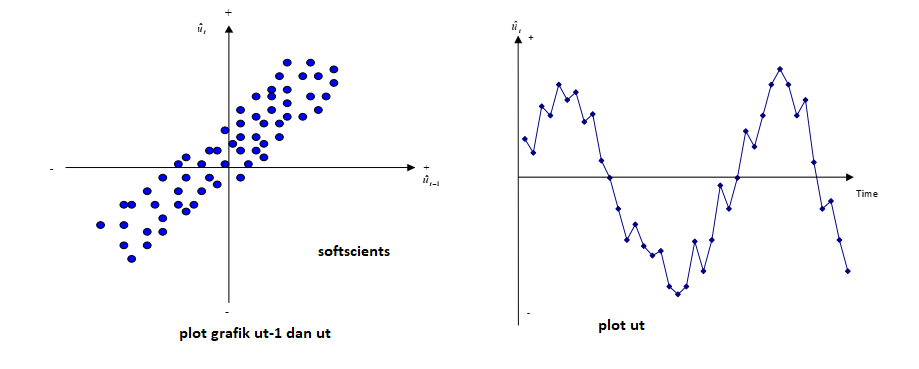
2. Autokorelasi negatif seperti grafik berikut

3. Sedangkan non korelasi seperti berikut

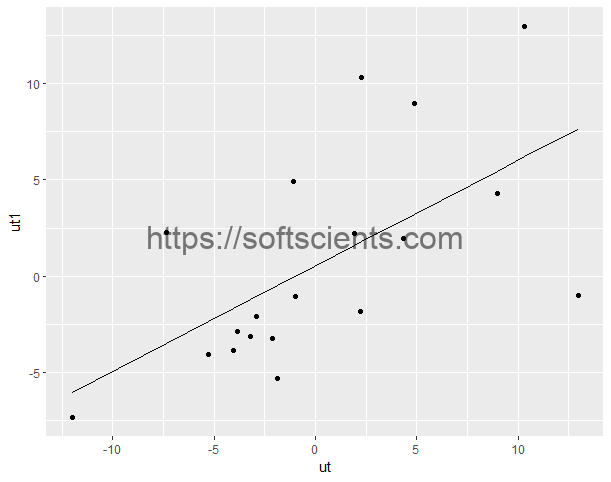
Namun terkadang akan sulit memahami sebuah plot grafik diatas, maka solusi analitik dapat menggunakan durbin watson. Kita kembali pada dataset diatas, bila kita plot residualnya.

model2 = lm(data=produksi2, ut1~ut)

ggplot() +
    geom_point(data = produksi2, aes(x=ut,y=ut1))+
    geom_line(data = produksi2, aes(x=ut,y = model2$fitted.values))

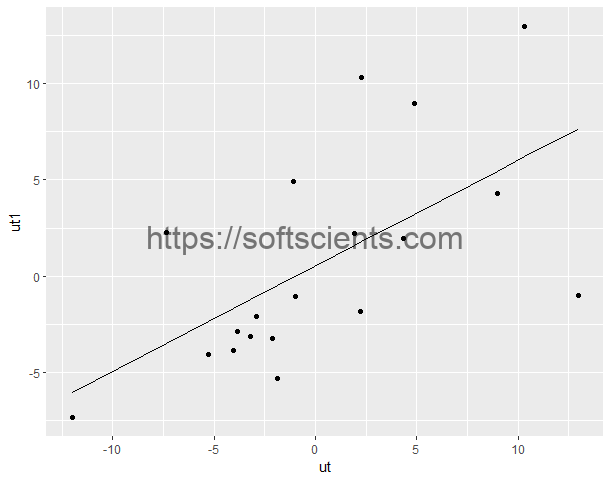
Artinya mempunyai hubungan korelasi positif,

Grafik ACF

Grafik ACF seperti berikut (kalian bisa lihat grafik autokorelasi positif diatas)

acf(model$residuals)

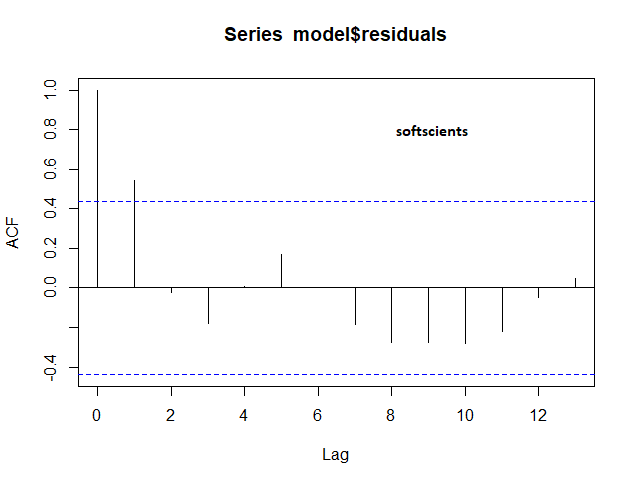
Kalian bisa lihat pada lag ke 1 melewati garis reratanya artinya ada korelasi pada lag 1 dengan nilai lebih dari 0.4, penjelasan mengenai ACF bisa kalian pelajari di Korelasi linear Pearson dan Fungsi Autokorelasi (ACF)

Statistik Uji Durbin-Watson

Metode ini hanya berlaku untuk model regresi yang variabel-variabel bebasnya tidak mengandung lagged dependent variable (time lag). Statistik Uji Durbin Watson tidak relevan digunakan dalam penaksiran model regresi yang menggunakan data cross section dan penaksiran model regresi tanpa intercept. Rumus untuk menghitung durbin-watson adalah

$d=\frac{\sum_{t=2}^{t=N}{(e_t-e_{t-1})^{2}}}{\sum_{t=1}^{t=N}{e_t^2}}$

$d$ adalah nilai durbin watson

$e_t$ adalah nilai residual

$e_{t-1}$ adalah nilai residul t-1 (periode sebelumnya)

Secara umum Interpretasi uji Durbin-Watson dapat dinyatakan sebagai berikut :

Dengan

dL : lower bound (batas bawah)

dU : upper bound (batas atas)

wilayah kritis

jika D>dU, gagal tolak H0

jika D<dL, tolak H0

jika dL <= D <= dU pengujian tidak meyakinkan

untuk menghitung durbin watson, kita butuh library lmtest, maka tambahkan berikut jangan lupa atau kalian harus install dulu

library(lmtest) #untuk durbin watson

Sedangkan perintah untuk menghitung durbin watson adalah

dwtest(Y ~ X, data = produksi)

hasil

   Durbin-Watson test

data:  Y ~ X
DW = 0.69655, p-value = 0.0001075
alternative hypothesis: true autocorrelation is greater than 0

diperoleh nilai statistik uji Durbin-Watson adalah sebesar 0,696550. Dari tabel Durbin Watson didapat bahwa nilai 𝑑𝐿 dan 𝑑𝑈 secara berturut-turut adalah 1,2015 dan 1,4107 dengan n=20 dan k =1 (Jumlah variabel bebas). Nilai statistik uji Durbin-Watson (0,696550) < 𝑑𝐿 (1,2015). Sehingga dapat disimpulkan bahwa terjadi autokorelasi positif pada data.

Download Tabel Durbin Watson

Silahkan kalian download tabel durbin watson https://lkeb.umm.ac.id/files/file/tabel-dw.pdf