Pengantar Metode Numerik

2,035 Views

Metode numerik merupakan mata kuliah wajib kalau kalian ambil jurusan ilmu komputer. Metode numerik kebanyakan membutuhkan looping/iterasi yang akan sulit diterapkan bila menggunakan excel, oleh sebab itu kebanyakan menggunakan bahasa pemrograman. Mengingat ini artikel yang cukup berat, saya ambil langsung dengan sedikit edit dari [1] ntar diakhir tulisan saya kasih contoh cara menghitung akar dari sebuah angka.

Gampang dong kalau saya kasih pertanyaan $y=\sqrt{9}$ , coba kalau dikasih pertanyaan $y = \sqrt{5}$ ? gimana cara hitung nya? Coba hitung pakai analitik. Yuk sekarang kita bahas saja Metode Numerik. Metode numerik merupakan teknik penyelesaian permasalahan yang diformulasikan secara matematis dengan menggunakan operasi hitungan (aritmatik) yaitu operasi tambah, kurang, kali, dan bagi. Metode ini digunakan karena banyak permasalahan matematis tidak dapat diselesaikan menggunakan metode analitik. Jikapun terdapat penyelesaiannya secara analitik, proses penyelesaiaannya sering kali cukup rumit dan memakan banyak waktu sehingga tidak efisien. Apalagi sekarang komputer sudah banyak perkembangan serta bahasa pemrograman yang gampang dipelajari, maka beberapa penyelesaian biasanya menggunakan metode numerik.

Terdapat keuntungan dan kerugian terkait penggunaan metode numerik. Keuntungan dari metode ini antara lain:

Solusi persoalan selalu dapat diperoleh.
Dengan bantuan komputer, perhitungan dapat dilakukan dengan cepat serta hasil yang diperoleh dapat dibuat sedekat mungkin dengan nilai sesungguhnya.
Tampilan hasil perhitungan dapat disimulasikan.

Adapun kelemahan metode ini antara lain:

Nilai yang diperoleh berupa pendekatan atau hampiran.
Tanpa bantuan komputer, proses perhitungan akan berlangsung lama dan berulang-ulang.

Perbedaan Antara Metode Numerik dan Analitik

Contents

1 Perbedaan Antara Metode Numerik dan Analitik
2 Tahapan Penyelesaian Menggunakan Metode Numerik
3 Akurasi dan Presisi
4 Error Numerik
5 Contoh Soal Metode Numerik

Perbedaan antara metode numerik dan metode analitik dapat dijelaskan sebagai berikut:

Solusi metode numerik selalu berbentuk angka, sedangkan solusi metode analitik dapat berbentuk fungsi matematik yang selanjutnya dapat dievaluasi untuk menghasilkan nilai dalam bentuk angka.
Solusi dari metode numerik berupa hampiran, sedangkan metode analitik berupa solusi sejati. Kondisi ini berakibat pada nilai error metode analitik adalah 0, sedangkan metode numerik ̸= 0. 3.
Metode analitik cocok untuk permasalahan dengan model terbatas dan sederhana, sedangkan metode numerik cocok dengan semua jenis permasalahan.

Tahapan Penyelesaian Menggunakan Metode Numerik

Terdapat beberapa tahapan dalam menyelesaikan suatu permasalahan dengan metode numerik. Tahapan-tahapan tersebut antara lain:

Pemodelan: Persoalan dunia nyata dimodelkan ke dalam persamaan matematika. Persamaan matematika yang terbentuk dapat berupa persamaan linier, non-linier, dan sebagainya sesuai dengan persoalan yang dihadapi.
Penyederhanaan Model: Model matematika yang dihasilkan dari tahap 1 mungkin saja terlalu kompleks. Semakin kompleks suatu model, semakin rumit penyelesaiaannya, sehingga model perlu disederhanakan. Seberapa sederhana model yang akan kita buat? tergantung pada permasalahan apa yang hendak pembaca selesaikan. Model yang terlalu sederhana akan tidak cocok digunakan untuk digunakan sebagai pendekatan sistem nyata atau lingkungan yang begitu kompleks. Penyederhanaan dapat berupa asumsi sejumlah variabel yang terlibat tidak signifikan, atau asumsi kondisi reaktor (steady atau non-steady).
Formulasi Numerik: Setelah model matematika sederhana diperoleh, tahap selanjutnya adalah memformulasikan model matematika secara numerik. Tahapan ini terdiri atas:
- menentukan metode numerik yang akan dipakai bersama-sama dengan analisis galat (error) awal.
- menyusun algoritma dari metode numerik yang dipilih.
Pemrograman: Tahap selanjutnya adalah menerjemahkan algoritma ke dalam program komputer. Pada tahapan ini pembaca bisa memilih bahasa pemrograman yang pembaca kuasai. Dalam buku ini kita hanya akan berfokus pada bahasa pemrograman R. Pembaca dapat menggunakan bahasa pemrograman lain selain dari buku ini. Pembaca hanya perlu memperhatikan bagaimana penulis membangun algoritma penyelesaian dan memtransfernya menjadi bentuk sintaks R. Dari sintaks tersebut pembaca dapat melihat bagaimana meletakakkan tiap tahapan algoritma menjadi sintaks pada bahasa pemrograman.
Operasional: Sebelum digunakan dengan data sesungguhnya, program komputer perlu dilakukan uji coba dengan data simulasi dan dievaluasi hasilnya. jika hasil keluaran diyakini sudah sesuai, baru dioperasikan dengan data yang sesungguhnya.
Evaluasi: Bila program sudah selesai dijalankan dengan data yang sesungguhnya, maka hasil yang diperoleh dilakukan interpretasi, meliputi analisis hasil keluaran dan membandingkannya dengan prinsip dasar dan hasil-hasil empriik untuk menaksir kualitas soluasi numerik termasuk keputusan untuk menjalankan kembali progrma dengan memperoleh hasil yang lebih baik.

Akurasi dan Presisi

Untuk memahami apa itu akurasi dan presisi perhatikan gambar berikut

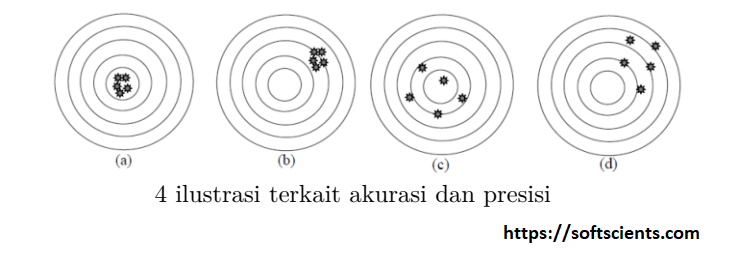
Gambar 1

Terdapat 4 buah kondisi ketika kita menembakkan beberapa perluru pada sebuah sasaran. Tujuan kita disini adalah untuk menembak bagian tengah sasaran tersebut. Dapat disimpulkan sebagai berikut

Akurat

Pada Gambar (a) dan (c) merupakan gambar yang menunjukkan seseorang telah berhasil mengenai bagian tengah sasaran tersebut dapat kita katakan pula tembakan pada kedua gambar tersebut akurat. Akurat dalam hal ini dapat diartikan suatu kondisi dimana kedekatan lubang peluru dengan pusat sasaran. Secara umum akurasi diartikan sebagai tingkat kedekatan pengukuran kuantitas terhadap nilai sebenarnya. Terdapat dua buah cara untuk mengukur akurasi.

Metode pengukuran akurasi antara lain: error absolut dan error relatif. Error absolut merupakan nilai absolut dari selisih antara nilai sebenarnya x dengan nilai observasi x′. Error absolut dapat dituliskan menggunakan Persamaan berikut

$\epsilon_A = |x-x'|$

Pengukuran lain yang sering digunakan untuk mengukur akurasi adalah error relatif. Berbeda dengan error absolut, error relatif membagi selisih antara nilai sebenarnya x dan nilai observasi x′ dengan nilai sebenarnya. Hasil yang diperoleh merupakan nilai tanpa satuan. Persamaan error relatif disajikan pada

$\epsilon_R = \frac{|x-x'|}{x}$

Dalam suatu pengukuran, hal lain yang perlu diperhatikan selain akurasi adalah presisi. Presisi adalah sejauh mana pengulangan pengukuran dalam kondisi yang tidak berubah mendapat hasil yang sama. Berdasarkan Gambar 1, Gambar (a) dan (b) menunjukkan kepresisian yang tinggi. Hal ini terlihat dari jarak antara lubang peluru yang saling berdekatan dan mengelompok.

Berdasarkan Gambar 1 dapat kita simpulkan bahwa dalam suatu sistem pengukuran akan terdapat 4 buah kondisi.

Pengukuran akurat dan presisi Gambar (a),
tidak akurat namun presisi Gambar (b),
akurat namun tidak presisi Gambar (c), dan
tidak akurat serta tidak presisi (Gambar (d).

Dari kondisi-kondisi tersebut, akan meuncul yang dinamakan error. Dalam analisa numerik error atau kesalahan menjadi hal yang perlu diperhatikan

Error Numerik

Kesalahan numerik merupakan error atau kesalahan yang timbul akibat adanya proses pendekatan atau hampiran. Kesalahan numerik terjadi karena tiga hal, antara lain:

Kesalahan bawaan (inherent error), merupakan kesalahan data yang timbul akibat adanya pengkuran, human error seperti kesalahan pencatatan, atau tidak memahami hukum-hukum fisik dari data yang diukur.
Kesalahan pembulatan (round-off error), adalah kesalahan yang terjadi karena adanya pembulatan. Contoh: 3,142857143… menjadi 3,14.
Kesalahan pemotongan (truncation error), adalah kesalahan yang ditimbulkan pada saat dilakukan pengurangan jumlah angka signifikan

Contoh Soal Metode Numerik

Sesuai janji saya diatas, kita akan mencoba menggunakan metode numerik untuk menghitung akar suatu bilangan. hem.. kalian mau menggunakan bahasa apa? saya pakai R/RStudio saja biar gampang. Algoritma yang digunakan yaitu (kalian bisa juga menggunakan methode newton-raphson melalui fungsi turunan)

tentukan nilai yang akan dihitung $n$
tentukan nilai hampiran/tebakan pertama yaitu $x_0$
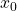
ulangi langkah berikut sampai nilai error nya kecil

$x_i = \frac{(x_i + \frac{n}{x_i})}{2}$

Yuk kita coba, tentuka nilai akar dari $y=\sqrt{9}$ dengan nilai tebakan awal yaitu $x_0=3.5$ . Langkah pertama kita buatkan dulu function

root<-function(n,x){
    y = (x+n/x)/2
    return (y)
}

Langkah kedua kita tentukan paramater dan nilai awal

x = 3.5 # tebakan awal
n = 9 #nilai yang dicari
iterasi = 5

Selanjutnya looping

for (i in c(1:iterasi)){
    y =  root(n,x)
    x = y
    print(paste("nilai x",i," yaitu ",x))
}

hasilnya

[1] "nilai x 1  yaitu  3.03571428571429"
[1] "nilai x 2  yaitu  3.00021008403361"
[1] "nilai x 3  yaitu  3.00000000735537"
[1] "nilai x 4  yaitu  3"
[1] "nilai x 5  yaitu  3"

Semakin banyak iterasi akan semakin menuju titik tertentu! Looping bisa mencapai ribuan, oleh sebab itu kita wajib menentukan error sebagai break looping, yuk kita perbaiki lagi untuk memasukan error absolut

for (i in c(1:iterasi)){
    y =  root(n,x)
    print(paste("nilai x",i," yaitu ",x))
    if(abs(y-x)==0){
        break
    }
    x = y

}

hasilnya menjadi berikut yaitu tidak sampai iterasi ke 5 namun looping berhenti di iterasi ke 4

[1] "nilai x 1  yaitu  3.03571428571429"
[1] "nilai x 2  yaitu  3.00021008403361"
[1] "nilai x 3  yaitu  3.00000000735537"
[1] "nilai x 4  yaitu  3"

Error sebaiknya jangan 0 tapi dibuat sedekat mungkin misalkan saja kita setting 0.0001, yuk kita coba kode berikut untuk menghitung $\sqrt{10}$

x = 5 # tebakan awal
n = 10 #nilai yang dicari
iterasi = 50
minimal_error = 1/1000
error_tiap_iterasi = c()
for (i in c(1:iterasi)){
    y =  root(n,x)
    print(paste("nilai x",i," yaitu ",x))
    error = abs(x-y)
    if(error<=minimal_error){
        break
    }
    x = y
    
}

Angkanya menuju konvergen

[1] "nilai x 1  yaitu  5"
[1] "nilai x 2  yaitu  3.5"
[1] "nilai x 3  yaitu  3.17857142857143"
[1] "nilai x 4  yaitu  3.16231942215088"

Mengingat ini hanya sebuah pengantar, maka untuk lebih jelasnya kalian baca-baca referensi dibawah ini

Perbedaan Antara Metode Numerik dan Analitik

Tahapan Penyelesaian Menggunakan Metode Numerik

Akurasi dan Presisi

Error Numerik

Contoh Soal Metode Numerik

Leave a Reply Cancel reply