
Untuk memahami apa kegunaan serta memahami gagasan umum tentang cara kerja Gradient descent dan persamaan matematika di baliknya, agar lebih mudah, saya menggunakan python sebagai ilustrasinya. Oiya kalian masih ingat donk mengenai pelajaran/kuliah mengenai kalkulus? yaitu mengenai limit, turunan /derivatif sebuah fungsi.
Apa itu Gradient Descent?
Contents
Jika kalian tidak terbiasa dengan istilah gradien descent / penurunan gradien yaitu adalah algoritma pengoptimalan untuk menemukan fungsi minimum yang bisa kalian tentukan secara mudah melalui penurunan sebuah function. Mengapa hal ini penting? Ingat pada bab sebelumnya kita menggunakan loss function fungsi ini sering disebut fungsi kerugian / biaya / fungsi tujuan/object function.
Mari kita mulai dengan eksperimen sederhana dengan melakukan perhitungan langsung di balik penurunan gradien , perhatikan persamaan kuadrat berikut
![]()
atau dalam persamaan turunan terhadap ![]() yaitu
yaitu
![]()
Mencari Nilai Minimum Fungsi dengan turunan
Berapa nilai minimum ![]() dan dengan membaca nilai dari plot? kalau dilihat dari plot diatas maka ada nilai 2
dan dengan membaca nilai dari plot? kalau dilihat dari plot diatas maka ada nilai 2 ![]() yaitu adalah
yaitu adalah ![]() dan
dan ![]() . Masih ingatkan? untuk menghitung diatas? yuk saya ajari caranya biar kalian sambil ingat pelajaran kelas 2 SMP.
. Masih ingatkan? untuk menghitung diatas? yuk saya ajari caranya biar kalian sambil ingat pelajaran kelas 2 SMP.
![]()
![]()
![]() dan
dan ![]()
jadi ketika ![]() atau
atau ![]() pada persamaan
pada persamaan ![]() , maka
, maka ![]() akan bernilai 0. Nah sekarang kita akan mencari nilai ujung/nilai y terendah/global minimum dari sebuah function diatas, kita butuh cara cepat yaitu menggunakan turunan fungsi
akan bernilai 0. Nah sekarang kita akan mencari nilai ujung/nilai y terendah/global minimum dari sebuah function diatas, kita butuh cara cepat yaitu menggunakan turunan fungsi
![]()
Pengertian Turunan Fungsi bisa kalian pelajari lengkap disini
Kalian baca saja pada Teorema 3 (Aturan Pangkat) yaitu jika ![]() maka
maka ![]() , dengan
, dengan ![]() adalah bilangan bulat positif maka
adalah bilangan bulat positif maka
![]()
sehingga persamaan
![]()
menjadi
![]()
untuk mencari ![]() ketika
ketika ![]() yaitu
yaitu
(1) 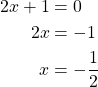
Sekarang nilai ![]() akan kita masukan ke persamaan
akan kita masukan ke persamaan
![]()
menghasilkan nilai ![]() . Yuk kita gambar langsung saja, kalian bisa melihat nilai global minimum nya
. Yuk kita gambar langsung saja, kalian bisa melihat nilai global minimum nya
Teknik iterasi
Nah setelah tahu cara kerja penggunaan turunan untuk mencari nilai global minimumnya, maka dengan teknik iterasi berikut yang sama kerjanya dengan loss function, kita akan mulai dengan nilai ![]() menghasilkan
menghasilkan ![]() , sesuai dengan plot grafik berikut, yang saya sebut dengan titik pencarian/starting point
, sesuai dengan plot grafik berikut, yang saya sebut dengan titik pencarian/starting point
Untuk mencari nilai y minimal, maka saya menggunakan rumus berikut
![]()
Dengan menggunakan persamaan diatas dimana:
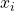 adalah nilai tebakan awal /starting point dalam hal ini kita pakai angka
adalah nilai tebakan awal /starting point dalam hal ini kita pakai angka 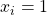
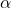 adalah nilai kecepatan pemelajaran (membuat “peluruhan lambat”)
adalah nilai kecepatan pemelajaran (membuat “peluruhan lambat”)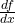 adalah turunan dari fungsi (berlawanan arah dengan turunan)
adalah turunan dari fungsi (berlawanan arah dengan turunan)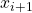 adalah nilai tebakan berikutnya
adalah nilai tebakan berikutnya
Kita akan cari tahu berapa nilai ![]() selanjutnya yaitu
selanjutnya yaitu
(2) 
Nilai
![]()
kita masukan ke
![]()
dihasilkan
![]()
kalian bisa melihat hasilnya, nilai x iterasi pertama akan semakin mendekati nilai global minimalnya
iterasi kedua
kita lanjutin
![]()
dimasukan kedalam persamaan berikut
(3) 
kita masukan ke
![]()
dihasilkan
![]()
kalian bisa melihat hasilnya, nilai x iterasi kedua akan semakin mendekati nilai global minimalnya
hal tersebut terus-menerus dilakukan sampai nilainya tidak berubah, yuk kita tulis algoritmanya
Penerapan Iterasi pada gradient descent
Untuk berhasil melakukan proses dengan benar, mari kita tulis program Python sederhana dan ikuti proses yang tercantum di bawah ini.
- Dapatkan fungsi objektif
- Inisialisasi secara acak nilai
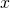 untuk memulai penurunan.
untuk memulai penurunan. - Tentukan kecepatan pembelajaran yang menentukan seberapa cepat kita akan konvergen ke minimum.
- Cari turunan dari nilai itu
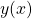 .
. - Perhitungan maju:
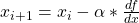
- Perbarui nilai lama dengan nilai baru:
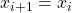
- Periksa kondisi berhenti/break. Jika syaratnya sudah terpenuhi, berhentilah yaitu tidak ada perbedaan antara nilai
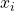 dengan
dengan 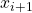 . Jika tidak, ulangi langkah 4.
. Jika tidak, ulangi langkah 4.
Yuk buat kode nya sesuai dengan algoritma diatas
xi = 1 #nilai x awal atau x0
alpha = 0.15 # konstanta pembelajaran
maksimal_iterasi = 10
target_error = 0.0001 # kondisi berhenti/error
# derivative dari function (x^2+x-6)
def derivative(x):
return 2*x+1
for iterasi in range (1,maksimal_iterasi+1):
x_current = xi
xi = xi - alpha * derivative(xi)
error = abs(xi - x_current)
print(f"Epoch: {iterasi}\t"
f" x: {x_current:.4f}\terror {error:.4f}")
if error < target_error:
break
hasilnya yaitu
Epoch: 1 x: 1.0000 error 0.4500 Epoch: 2 x: 0.5500 error 0.3150 Epoch: 3 x: 0.2350 error 0.2205 Epoch: 4 x: 0.0145 error 0.1543 Epoch: 5 x: -0.1398 error 0.1080 Epoch: 6 x: -0.2479 error 0.0756 Epoch: 7 x: -0.3235 error 0.0529 Epoch: 8 x: -0.3765 error 0.0371 Epoch: 9 x: -0.4135 error 0.0259 Epoch: 10 x: -0.4395 error 0.0182
kalian bisa lihat hasilnya akan semakin menuju ke ![]()
Atau kalian bisa menggunakan Octave agar lebih mudah dalam melihat grafiknya
clc;clear all;close all;
xi = 1;
alpha = 0.15;
maksimal_iterasi = 10;
target_error = 0.0001;
derivatif = @(x) 2*x+1;
for i=1:maksimal_iterasi
x_current = xi;
xi = xi-alpha*derivatif(xi);
error(i) = abs(xi-x_current);
result(i) = xi;
if error<target_error
break
endif
endfor
figure,
subplot(1,2,1),plot(result),title(['nilai maksimal ' num2str(result(end))],'fontsize',18),
ylabel('nilai maksimal','fontsize',18);
grid on;
subplot(1,2,2),plot(error),title('Error','fontsize',18),xlabel('iterasi','fontsize',18),
ylabel('iterasi','fontsize',18);
grid on;

Oiya dalam blog ini, saya tidak hanya saja menggunakan Python-numpy-matplolib tapi juga menggunakan octave agar lebih ringkas kodenya. Bila kalian ingin belajar Octave, bisa lihat buku saya disini
Atau kalian bisa menggunakan tensor dengan library tensorflow untuk menghitung gradient descent, disini
Atau kalian bisa baca PyTorch Backward dan Step Optimizer serta membuat MLP terlebih dahulu sebelum menggunakan teknik iterasi menggunakan pytorch sebagai berikut
import numpy as np
import torch
a = np.array([1],dtype=np.float32) #tebakan awal x= 1
for i in range(0,1000):
x = torch.tensor(a,requires_grad=True)
y = x**2+x-6
y.backward()
optim = torch.optim.SGD([x],lr=0.15)
optim.step()
print(x) #akan menuju -0.5
a = x.detach().numpy()
outputnya yaitu
0 tensor([0.5500], requires_grad=True) 1 tensor([0.2350], requires_grad=True) 2 tensor([0.0145], requires_grad=True) 3 tensor([-0.1399], requires_grad=True) 4 tensor([-0.2479], requires_grad=True) 5 tensor([-0.3235], requires_grad=True) 6 tensor([-0.3765], requires_grad=True) 7 tensor([-0.4135], requires_grad=True) 8 tensor([-0.4395], requires_grad=True) 9 tensor([-0.4576], requires_grad=True) 10 tensor([-0.4703], requires_grad=True) 11 tensor([-0.4792], requires_grad=True) 12 tensor([-0.4855], requires_grad=True) 13 tensor([-0.4898], requires_grad=True) 14 tensor([-0.4929], requires_grad=True) 15 tensor([-0.4950], requires_grad=True) 16 tensor([-0.4965], requires_grad=True) 17 tensor([-0.4976], requires_grad=True) 18 tensor([-0.4983], requires_grad=True) 19 tensor([-0.4988], requires_grad=True) 20 tensor([-0.4992], requires_grad=True) 21 tensor([-0.4994], requires_grad=True) 22 tensor([-0.4996], requires_grad=True) 23 tensor([-0.4997], requires_grad=True) 24 tensor([-0.4998], requires_grad=True) 25 tensor([-0.4999], requires_grad=True) 26 tensor([-0.4999], requires_grad=True) 27 tensor([-0.4999], requires_grad=True) 28 tensor([-0.5000], requires_grad=True) 29 tensor([-0.5000], requires_grad=True) 30 tensor([-0.5000], requires_grad=True) 31 tensor([-0.5000], requires_grad=True)
Selesai….
